Giải online hệ phương trình phi tuyến
Giải hệ phương trình phi tuyến bằng phương pháp số
Nếu sau nhiều lần thử mà vẫn "not found" thì cần thiết phải gán các giá trị ban đầu Initials!
Nhập vào:
+ Biến: x0, x1, x2, ... ; hoặc x,y,z,t,u,v,w;
+ Mỗi phương trình trên một dòng.
+ Giá trị ban đầu Initials tùy chọn (phân cách bởi khoảng trống).
+ Số PI (π=3.1415926...)
+ Dấu ngoặc ()
+ Phép toán + - * / ^
+ Các hàm ABS SIN COS TAN COTAN LOG LOG10 SIGN TRUNCATE
Thí dụ:
Tìm nghiệm hệ phương trình
x^3*y-y^4=7
x^2*y+2*x*y^2+y^3=9
Nhập vào dạng các biến là x0, x1, x2...:
x0^3*x1-x1^4-7
x0^2*x1+2*x0*x1^2+x1^3-9
hoặc sử dụng các biến là x,y,z...:
x^3*y-y^4-7
x^2*y+2*x*y^2+y^3-9
Initials như là: 2 7
Màn hình chương trình
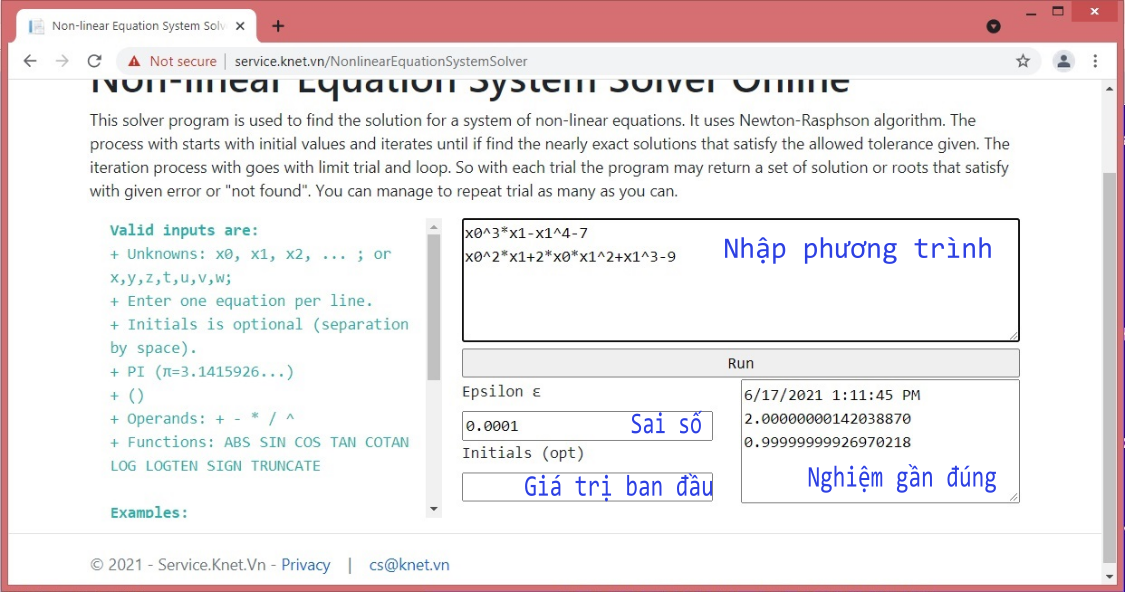
Keywords: Giải hệ phương trình phi tuyến bằng phương pháp số; Solve a system of non-linear equations online;
